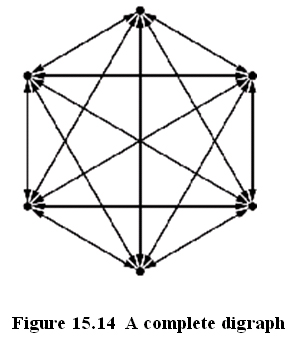
The Complete Digraph on Six Vertices

The graph shown in Figure 15.14 is the complete digraph on six vertices. It has 15 double-directed edges, so the total number of (one-way) edges is 30, which is n(n –1) = 6(6– 1) = 6(5) = 30.

Theorem. The number of edges in the complete digraph on n vertices is n(n –1).
There are n(n –1)/2 undirected edges on the corresponding complete undirected graph. That makes n (n –1)/2 double-directed edges, so the total number of (one-way) directed edges must be twice that number.
 

The number of edges in any digraph on n vertices is m n (n –1).

Every digraph has an embedded graph, obtained by converting each directed edge into an undirected edge and then removing duplicate edges and loops. Mathematically, this amounts to converting each ordered pair (x, y) of vertices in E into the set {x, y} and then removing all sets of size one (i.e., singletons).

It took me a long time to type

Source: Schaum's Outline of Data Structures with Java 2nd Edition
by John R. Hubbard